[ad_1]
Determine 1: stepwise behavior in self-supervised understanding. When coaching frequent SSL algorithms, we locate that the decline descends in a stepwise style (top remaining) and the acquired embeddings iteratively increase in dimensionality (bottom remaining). Immediate visualization of embeddings (suitable best a few PCA directions revealed) confirms that embeddings are initially collapsed to a place, which then expands to a 1D manifold, a 2D manifold, and over and above concurrently with measures in the loss.
It is widely believed that deep learning’s stunning good results is owing in aspect to its skill to discover and extract practical representations of advanced data. Self-supervised finding out (SSL) has emerged as a foremost framework for finding out these representations for visuals specifically from unlabeled information, related to how LLMs master representations for language directly from internet-scraped text. Yet regardless of SSL’s crucial role in condition-of-the-art styles these as CLIP and MidJourney, essential issues like “what are self-supervised picture methods genuinely studying?” and “how does that studying essentially occur?” lack simple answers.
Our new paper (to show up at ICML 2023) provides what we suggest is the very first powerful mathematical photograph of the training system of big-scale SSL techniques. Our simplified theoretical product, which we address specifically, learns areas of the information in a sequence of discrete, very well-divided techniques. We then reveal that this behavior can be observed in the wild across many current point out-of-the-art techniques.
This discovery opens new avenues for improving SSL solutions, and permits a complete variety of new scientific inquiries that, when answered, will deliver a highly effective lens for understanding some of today’s most crucial deep mastering programs.
Track record
We concentrate in this article on joint-embedding SSL strategies — a superset of contrastive techniques — which understand representations that obey look at-invariance requirements. The decline function of these products contains a phrase implementing matching embeddings for semantically equivalent “views” of an image. Remarkably, this basic strategy yields powerful representations on impression jobs even when sights are as very simple as random crops and colour perturbations.
Concept: stepwise finding out in SSL with linearized products
We initial explain an just solvable linear model of SSL in which each the schooling trajectories and final embeddings can be written in closed form. Notably, we obtain that illustration discovering separates into a series of discrete techniques: the rank of the embeddings starts off tiny and iteratively boosts in a stepwise studying system.
The most important theoretical contribution of our paper is to exactly resolve the training dynamics of the Barlow Twins loss operate beneath gradient movement for the particular situation of a linear design (mathbff(mathbfx) = mathbfW mathbfx). To sketch our conclusions listed here, we uncover that, when initialization is little, the design learns representations composed exactly of the prime-(d) eigendirections of the featurewise cross-correlation matrix (boldsymbolGamma equiv mathbbE_mathbfx,mathbfx’ [ \mathbfx \mathbfx’^T ]). What is additional, we obtain that these eigendirections are acquired a person at a time in a sequence of discrete understanding ways at instances decided by their corresponding eigenvalues. Determine 2 illustrates this finding out method, displaying both of those the growth of a new route in the represented perform and the resulting drop in the loss at each and every mastering move. As an extra bonus, we come across a shut-sort equation for the final embeddings figured out by the product at convergence.
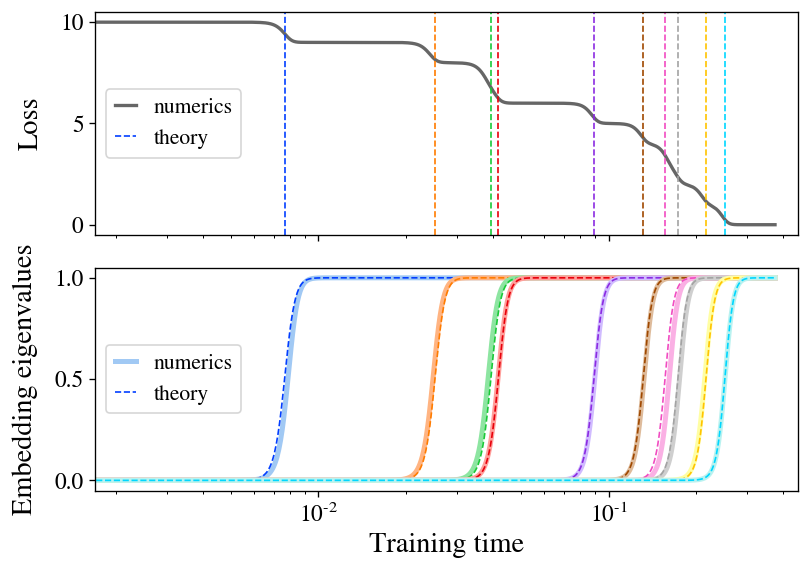
Determine 2: stepwise finding out seems in a linear model of SSL. We teach a linear design with the Barlow Twins decline on a compact sample of CIFAR-10. The loss (top) descends in a staircase fashion, with phase moments effectively-predicted by our theory (dashed lines). The embedding eigenvalues (bottom) spring up a person at a time, closely matching theory (dashed curves).
Our acquiring of stepwise learning is a manifestation of the broader idea of spectral bias, which is the observation that several finding out units with roughly linear dynamics preferentially discover eigendirections with better eigenvalue. This has not too long ago been properly-examined in the situation of common supervised mastering, where by it is been uncovered that increased-eigenvalue eigenmodes are acquired a lot quicker throughout coaching. Our function finds the analogous benefits for SSL.
The reason a linear product deserves thorough review is that, as revealed by way of the “neural tangent kernel” (NTK) line of function, adequately extensive neural networks also have linear parameterwise dynamics. This actuality is sufficient to prolong our solution for a linear model to huge neural nets (or in actuality to arbitrary kernel equipment), in which scenario the product preferentially learns the top rated (d) eigendirections of a distinct operator linked to the NTK. The analyze of the NTK has yielded a lot of insights into the schooling and generalization of even nonlinear neural networks, which is a clue that possibly some of the insights we’ve gleaned could possibly transfer to reasonable conditions.
Experiment: stepwise learning in SSL with ResNets
As our major experiments, we coach several major SSL procedures with comprehensive-scale ResNet-50 encoders and find that, remarkably, we obviously see this stepwise finding out sample even in real looking configurations, suggesting that this actions is central to the understanding actions of SSL.
To see stepwise discovering with ResNets in realistic setups, all we have to do is run the algorithm and observe the eigenvalues of the embedding covariance matrix above time. In exercise, it aids highlight the stepwise conduct to also teach from smaller sized-than-typical parameter-smart initialization and coach with a small understanding price, so we’ll use these modifications in the experiments we chat about right here and explore the typical scenario in our paper.
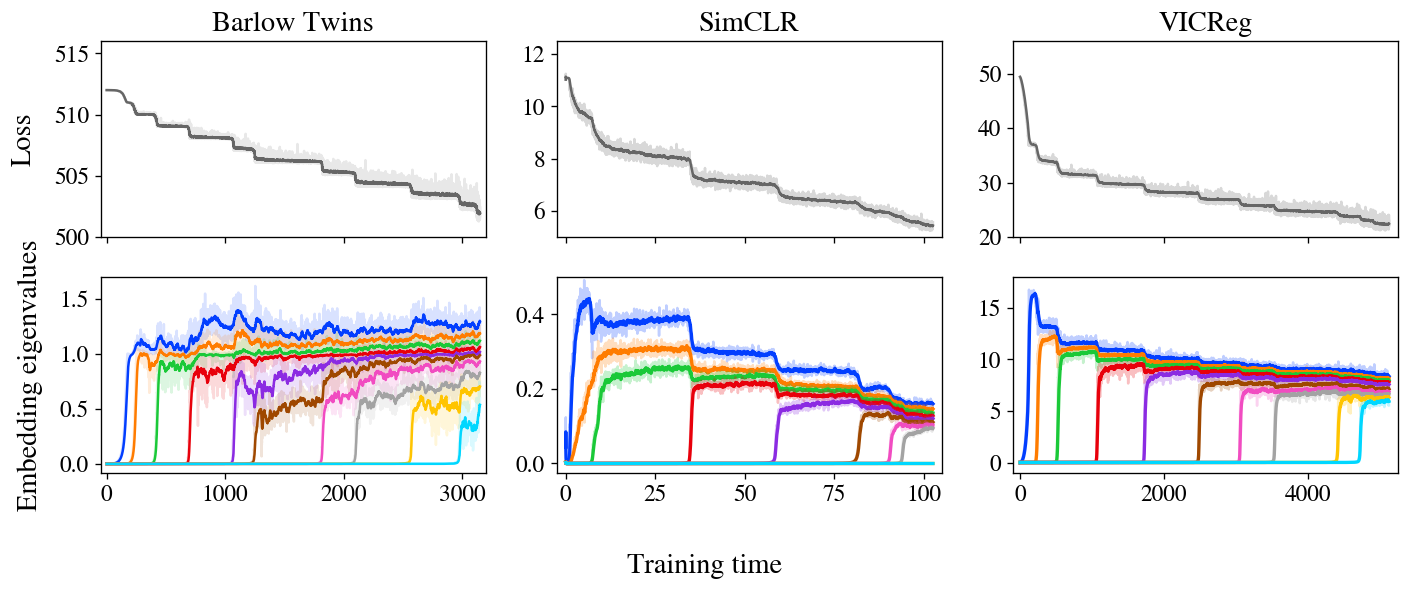
Determine 3: stepwise discovering is clear in Barlow Twins, SimCLR, and VICReg. The loss and embeddings of all a few approaches display stepwise mastering, with embeddings iteratively raising in rank as predicted by our design.
Determine 3 shows losses and embedding covariance eigenvalues for 3 SSL techniques — Barlow Twins, SimCLR, and VICReg — skilled on the STL-10 dataset with typical augmentations. Remarkably, all a few present extremely distinct stepwise mastering, with decline lowering in a staircase curve and a single new eigenvalue springing up from zero at just about every subsequent phase. We also exhibit an animated zoom-in on the early actions of Barlow Twins in Figure 1.
It is value noting that, when these a few approaches are somewhat distinctive at initially look, it is been suspected in folklore for some time that they are executing a thing similar underneath the hood. In individual, these and other joint-embedding SSL solutions all realize related efficiency on benchmark tasks. The obstacle, then, is to establish the shared conduct fundamental these diversified strategies. Considerably prior theoretical work has targeted on analytical similarities in their loss features, but our experiments suggest a different unifying basic principle: SSL solutions all study embeddings just one dimension at a time, iteratively adding new dimensions in get of salience.
In a past incipient but promising experiment, we assess the genuine embeddings learned by these procedures with theoretical predictions computed from the NTK just after education. We not only obtain great settlement between theory and experiment within each and every approach, but we also review throughout approaches and uncover that distinctive approaches study related embeddings, including more support to the idea that these approaches are eventually accomplishing similar items and can be unified.
Why it matters
Our do the job paints a fundamental theoretical photo of the approach by which SSL methods assemble acquired representations around the system of teaching. Now that we have a theory, what can we do with it? We see assure for this photo to the two support the observe of SSL from an engineering standpoint and to help far better comprehending of SSL and probably representation learning a lot more broadly.
On the realistic aspect, SSL types are famously gradual to educate as opposed to supervised education, and the cause for this difference isn’t regarded. Our picture of schooling suggests that SSL instruction requires a extensive time to converge due to the fact the later on eigenmodes have very long time constants and choose a long time to develop noticeably. If that picture’s ideal, rushing up education would be as basic as selectively concentrating gradient on modest embedding eigendirections in an endeavor to pull them up to the amount of the others, which can be finished in basic principle with just a very simple modification to the reduction functionality or the optimizer. We examine these prospects in additional depth in our paper.
On the scientific aspect, the framework of SSL as an iterative process permits a single to question lots of issues about the unique eigenmodes. Are the ones acquired first extra helpful than the types acquired later? How do diverse augmentations change the acquired modes, and does this count on the precise SSL process employed? Can we assign semantic articles to any (subset of) eigenmodes? (For case in point, we have noticed that the initially handful of modes learned often represent remarkably interpretable functions like an image’s regular hue and saturation.) If other types of illustration studying converge to comparable representations — a simple fact which is quickly testable — then solutions to these issues might have implications extending to deep finding out much more broadly.
All thought of, we’re optimistic about the potential clients of long run perform in the region. Deep discovering continues to be a grand theoretical thriller, but we feel our conclusions listed here give a handy foothold for long run experiments into the learning behavior of deep networks.
This post is centered on the paper “On the Stepwise Character of Self-Supervised Learning”, which is joint perform with Maksis Knutins, Liu Ziyin, Daniel Geisz, and Joshua Albrecht. This function was conducted with Usually Clever exactly where Jamie Simon is a Investigate Fellow. This blogpost is cross-posted below. We’d be delighted to field your questions or remarks.
[ad_2]
Resource link

