[ad_1]
Deep neural networks have enabled technological wonders ranging from voice recognition to device changeover to protein engineering, but their layout and application is even so notoriously unprincipled.
The development of instruments and strategies to guidebook this process is one particular of the grand problems of deep learning concept.
In Reverse Engineering the Neural Tangent Kernel, we propose a paradigm for bringing some basic principle to the artwork of architecture design and style working with latest theoretical breakthroughs: to start with layout a fantastic kernel function – usually a much less difficult job – and then “reverse-engineer” a internet-kernel equivalence to translate the selected kernel into a neural community.
Our primary theoretical end result allows the layout of activation features from first ideas, and we use it to generate just one activation perform that mimics deep (textrmReLU) community general performance with just a person hidden layer and an additional that soundly outperforms deep (textrmReLU) networks on a artificial job.
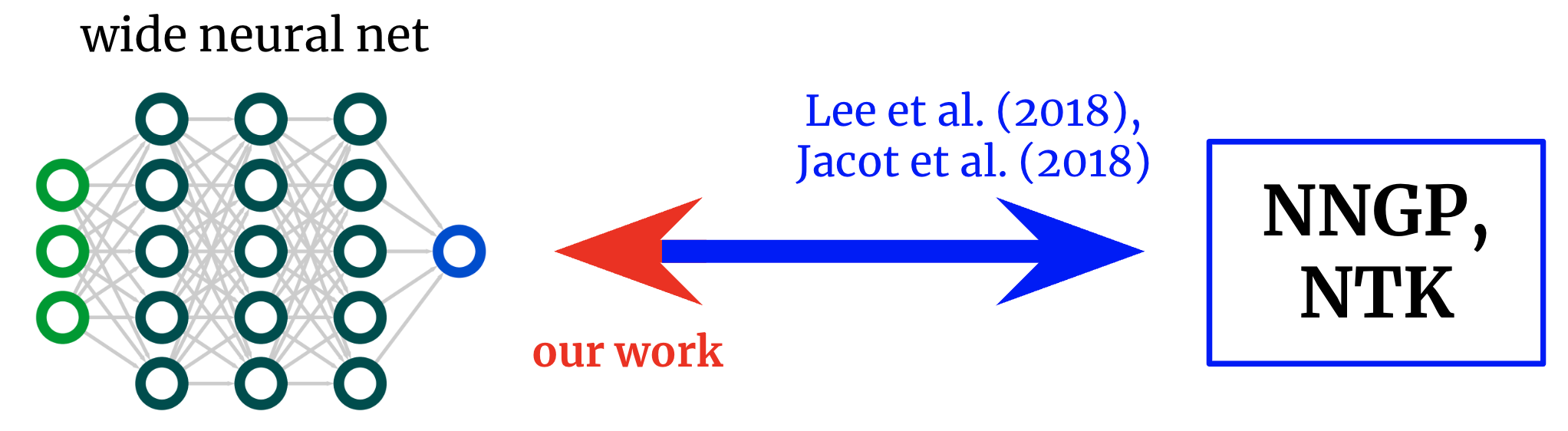
Kernels again to networks. Foundational is effective derived formulae that map from wide neural networks to their corresponding kernels. We receive an inverse mapping, permitting us to get started from a wished-for kernel and flip it back again into a community architecture.
Neural network kernels
The area of deep learning theory has recently been reworked by the realization that deep neural networks generally turn out to be analytically tractable to examine in the infinite-width limit.
Consider the limit a particular way, and the network in truth converges to an everyday kernel approach working with possibly the architecture’s “neural tangent kernel” (NTK) or, if only the last layer is qualified (a la random aspect models), its “neural network Gaussian process” (NNGP) kernel.
Like the central limit theorem, these vast-community limits are often shockingly good approximations even considerably from infinite width (often holding correct at widths in the hundreds or 1000’s), supplying a impressive analytical handle on the mysteries of deep studying.
From networks to kernels and again once more
The original will work checking out this net-kernel correspondence gave formulae for going from architecture to kernel: given a description of an architecture (e.g. depth and activation perform), they give you the network’s two kernels.
This has permitted fantastic insights into the optimization and generalization of several architectures of interest.
Nevertheless, if our objective is not just to recognize existing architectures but to style new kinds, then we may possibly alternatively have the mapping in the reverse direction: supplied a kernel we want, can we discover an architecture that gives it to us?
In this perform, we derive this inverse mapping for fully-connected networks (FCNs), allowing for us to design and style very simple networks in a principled fashion by (a) positing a sought after kernel and (b) designing an activation operate that gives it.
To see why this can make feeling, let us first visualize an NTK.
Consider a wide FCN’s NTK (K(x_1,x_2)) on two input vectors (x_1) and (x_2) (which we will for simplicity believe are normalized to the same size).
For a FCN, this kernel is rotation-invariant in the sense that (K(x_1,x_2) = K(c)), exactly where (c) is the cosine of the angle in between the inputs.
Given that (K(c)) is a scalar purpose of a scalar argument, we can basically plot it.
Fig. 2 exhibits the NTK of a four-concealed-layer (4HL) (textrmReLU) FCN.
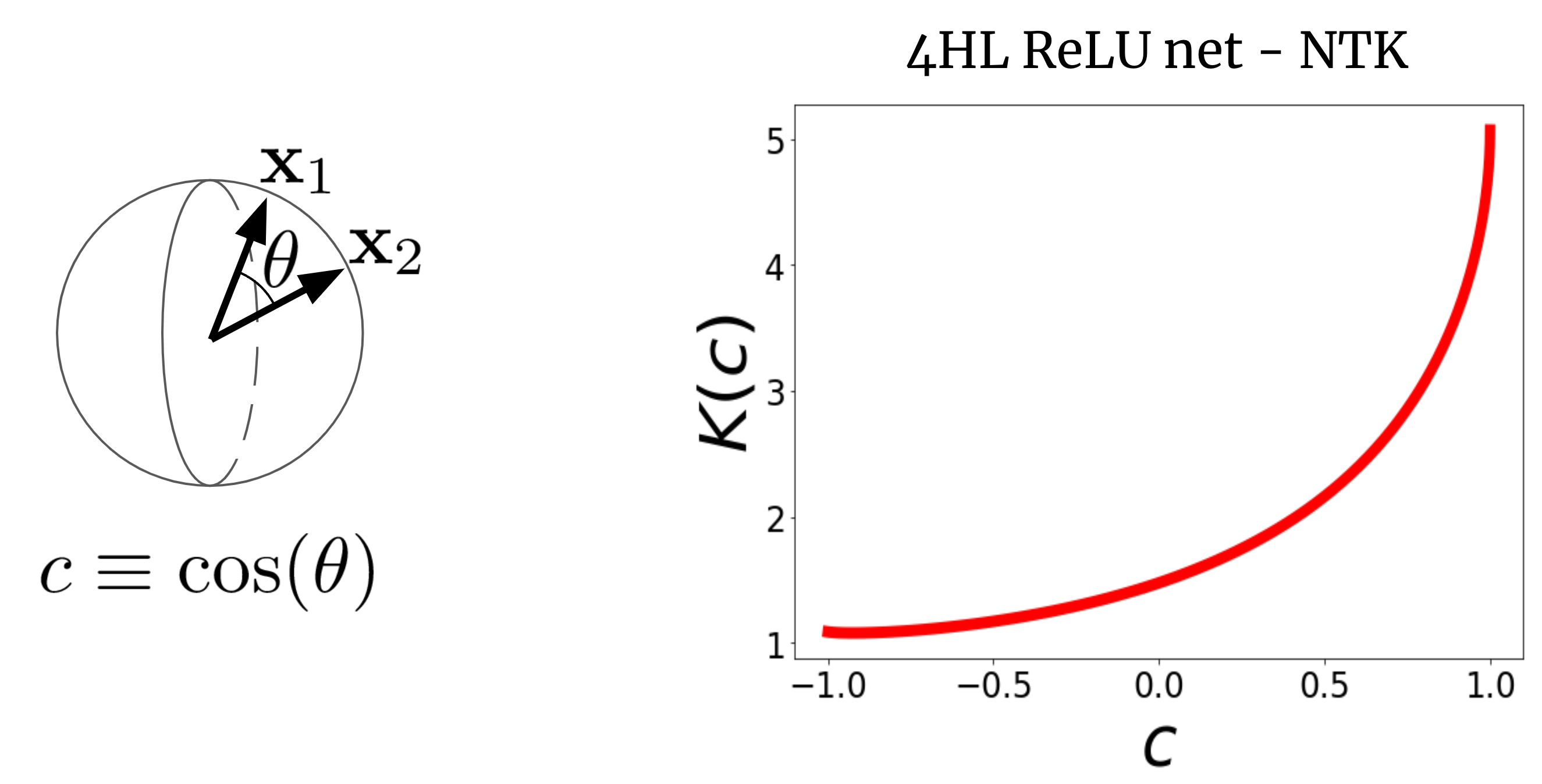
Fig 2. The NTK of a 4HL $textrmReLU$ FCN as a purpose of the cosine concerning two input vectors $x_1$ and $x_2$.
This plot basically is made up of much details about the mastering behavior of the corresponding large community!
The monotonic enhance implies that this kernel expects closer details to have a lot more correlated function values.
The steep improve at the conclusion tells us that the correlation size is not as well significant, and it can fit sophisticated functions.
The diverging derivative at (c=1) tells us about the smoothness of the function we be expecting to get.
Importantly, none of these details are apparent from wanting at a plot of (textrmReLU(z))!
We claim that, if we want to understand the effect of deciding upon an activation function (phi), then the ensuing NTK is essentially far more enlightening than (phi) itself.
It therefore possibly can make sense to test to layout architectures in “kernel area,” then translate them to the standard hyperparameters.
An activation perform for each and every kernel
Our key final result is a “reverse engineering theorem” that states the subsequent:
Thm 1: For any kernel $K(c)$, we can construct an activation purpose $tildephi$ such that, when inserted into a one-hidden-layer FCN, its infinite-width NTK or NNGP kernel is $K(c)$.
We give an express formulation for (tildephi) in terms of Hermite polynomials
(although we use a various purposeful variety in exercise for trainability explanations).
Our proposed use of this final result is that, in troubles with some regarded structure, it’ll sometimes be doable to write down a excellent kernel and reverse-engineer it into a trainable network with various pros in excess of pure kernel regression, like computational effectiveness and the ability to learn characteristics.
As a proof of strategy, we examination this strategy out on the artificial parity dilemma (i.e., presented a bitstring, is the sum odd or even?), immediately creating an activation purpose that substantially outperforms (textReLU) on the activity.
One hidden layer is all you need to have?
Here’s an additional surprising use of our final result.
The kernel curve previously mentioned is for a 4HL (textrmReLU) FCN, but I claimed that we can reach any kernel, including that a single, with just one hidden layer.
This indicates we can come up with some new activation purpose (tildephi) that gives this “deep” NTK in a shallow network!
Fig. 3 illustrates this experiment.
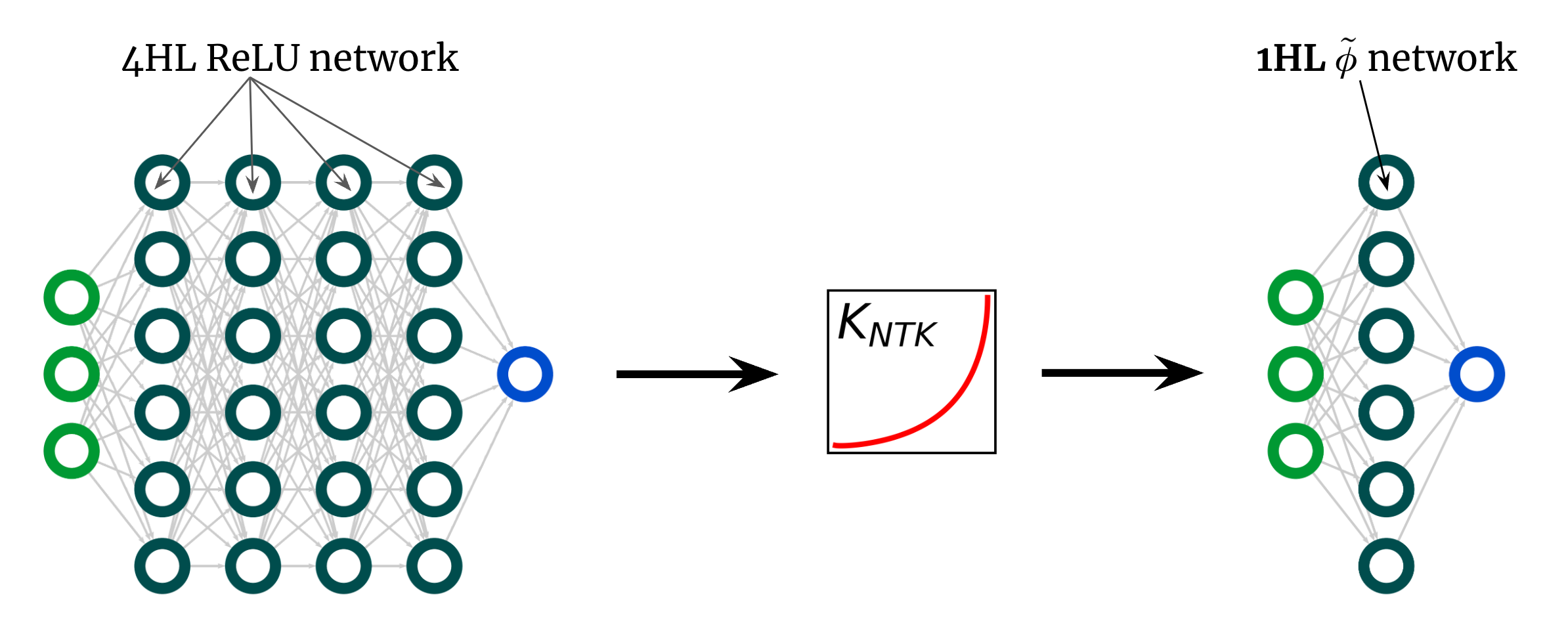
Fig 3. Shallowification of a deep $textrmReLU$ FCN into a 1HL FCN with an engineered activation functionality $tildephi$.
Shockingly, this “shallowfication” truly will work.
The still left subplot of Fig. 4 beneath exhibits a “mimic” activation purpose (tildephi) that provides almost the identical NTK as a deep (textrmReLU) FCN.
The appropriate plots then exhibit prepare + examination decline + precision traces for three FCNs on a conventional tabular dilemma from the UCI dataset.
Take note that, while the shallow and deep ReLU networks have really distinctive behaviors, our engineered shallow mimic community tracks the deep community nearly just!
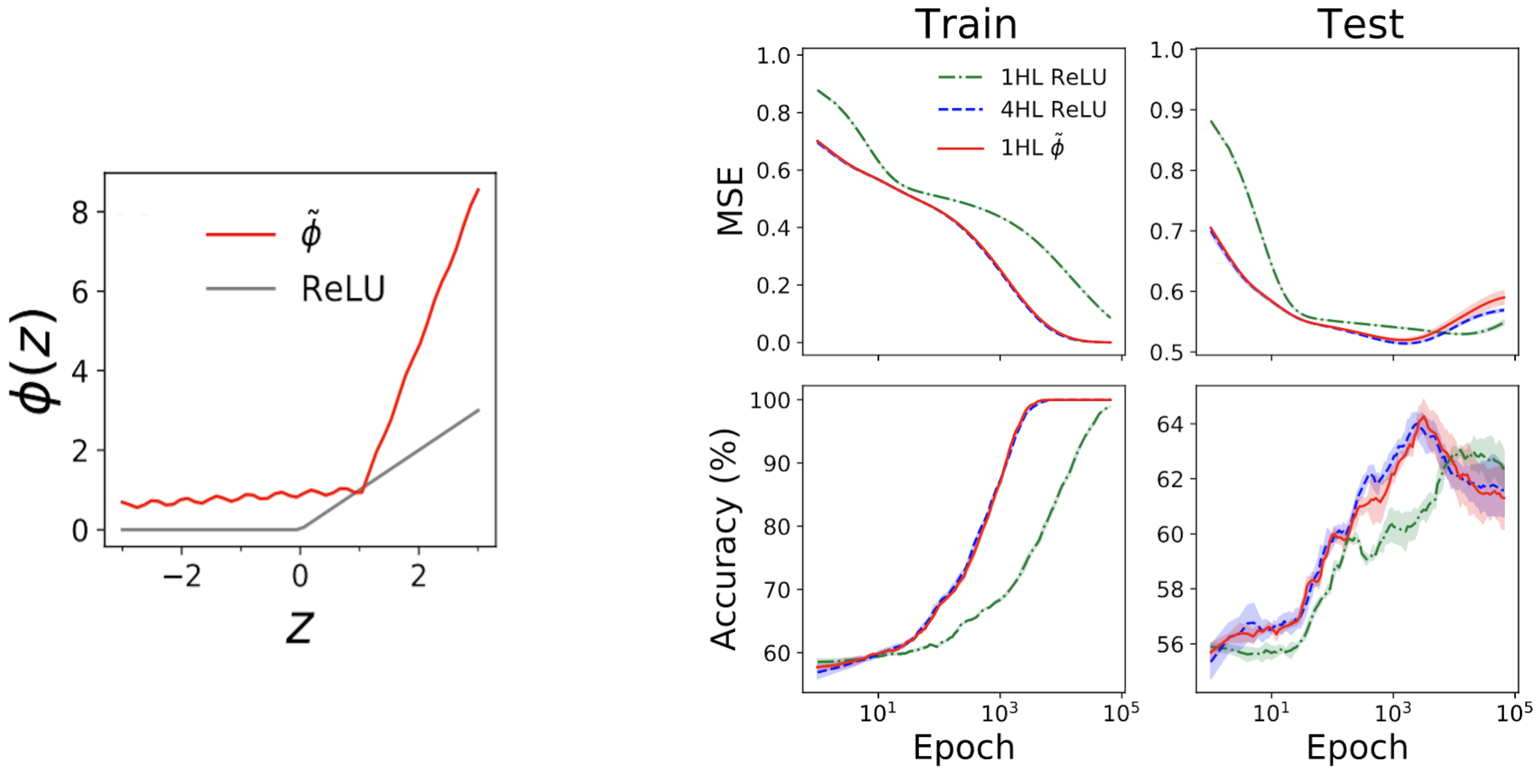
Fig 4. Remaining panel: our engineered “mimic” activation purpose, plotted with ReLU for comparison. Suitable panels: overall performance traces for 1HL ReLU, 4HL ReLU, and 1HL mimic FCNs qualified on a UCI dataset. Take note the shut match in between the 4HL ReLU and 1HL mimic networks.
This is exciting from an engineering standpoint because the shallow community uses fewer parameters than the deep community to attain the identical efficiency.
It’s also interesting from a theoretical viewpoint due to the fact it raises elementary inquiries about the value of depth.
A prevalent belief deep discovering belief is that further is not only far better but qualitatively various: that deep networks will efficiently learn capabilities that shallow networks only simply cannot.
Our shallowification outcome indicates that, at least for FCNs, this isn’t real: if we know what we’re undertaking, then depth doesn’t acquire us everything.
Conclusion
This perform arrives with loads of caveats.
The most important is that our final result only applies to FCNs, which alone are hardly ever condition-of-the-artwork.
Nonetheless, do the job on convolutional NTKs is fast progressing, and we imagine this paradigm of designing networks by planning kernels is ripe for extension in some form to these structured architectures.
Theoretical work has so significantly furnished reasonably number of resources for realistic deep studying theorists.
We goal for this to be a modest phase in that direction.
Even without the need of a science to guideline their design and style, neural networks have presently enabled wonders.
Just envision what we’ll be capable to do with them as soon as we ultimately have one.
This article is dependent on the paper “Reverse Engineering the Neural Tangent Kernel,” which is joint function with Sajant Anand and Mike DeWeese. We provide code to reproduce all our effects. We’d be delighted to industry your questions or opinions.
[ad_2]
Source backlink